AK Statistical/Data Science Journey

"We simulate things, not because it is hard, but because Math is sometimes harder to do or explain to others." – JFK if he had been an applied statistician

recent posts

about

  • Simulations are your friend! Part II: exploring the dangers of batch effects

    There’s a lot of diversity in project complexity where I work, but almost all of the projects start from comparing two or more groups of people. Sometimes the data come from the same source and can be processed around the same time, but for cases where samples are collected at different locations, or are too large to be processed at the same time, the issue of batch effects has to be addressed. The goal of these projects is often to find molecular features that are different between the groups of interest that are due to biology, and not because some of the samples of one group systemically received some noise (i.e. batch effect) that made them look different. To show-case when it’s possible to separate the signal (i.e. the true biological difference) from the noise, and when it’s not possible to do, I’ve found that some simple simulations can be helpful!

    Scenario 1: Suppose you have two groups of people. One group receives a treatment and another is only given a placebo. At the end of a trial, you measure some feature of the two groups and want to know if the treatment caused a notable difference compared to the placebos. However, you decide to sequence the placebo group and the treated group in two completely separate batches! If the true treatment effect is 0 (i.e. the groups are not different with respect to the feature you are measuring), what could go wrong? To show-case this, I simulated 50 placebos and controls, where both have their observed feature values (before batch effects) drawn from the same normal distribution N(\mu_{biol}, 1). But then I add batch effect noise to the placebos from a different normal distribution N(\mu_{batch1}, 1), and the treated group has their own distinct batch effect from a normal distribution N(\mu_{batch2}, 1). For some clarity, I’ll let the mean batch effects be far enough apart to create different peaks of observed points (say, \mu_{batch1} = 2 and \mu_{batch2} = 10). 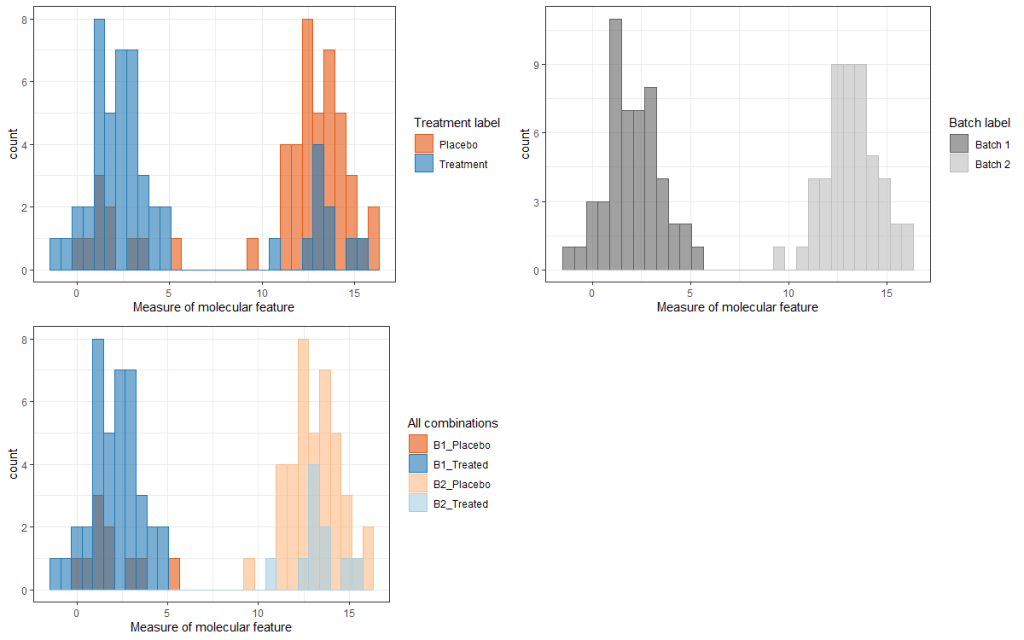Then we run either a t-test or a linear model, where the latter is run with just the treatment variable as a predictor and the molecular feature as our response. What should we expect to happen if we ran this set up through 1,000 simulations? I suspected that, because the two groups were created with very distinct batch effects, the t-test/simple linear models run in each simulation would detect this batch effect and not be able to parse effect. Hence, a large fraction of the simulations should return p-values for the treatment effect that were below the typical .05 threshold, and (fortunately for me) this time that’s exactly what happened! Roughly 90% (sometimes higher if the batch effect is large enough) of the simulations returned a p-value < .05. Furthermore, because the true treatment effect is 0, this corresponds to a false positive rate (FPR) of 0.9, well above our intended level of .05. Why does this occur? It’s because the treatment and placebos are sequenced in completely different batches, and the batch effects are (in this case) truly different from each other. Without mixing treated and control samples across the two batches, we can’t separate the treatment effect from the batch effect, and the latter is strong enough to create false positive results. The graph below shows this well, where the first picture (top left) show clear separation between the treatment and placebo groups (even though the true treatment effect difference is 0). The second plot (top right) shows the same separation when coloring by batches, which (in this scenario) is the real driver of differences observed among the treated and placebo groups (see bottom left). The choice of making the batch colors the same as the treated colors was intentional, if perhaps confusing. I wanted to emphasize that they share the same information, because there are no cases where a treated patient is not from the first batch, and no cases where a placebo is not from the second batch. This lack of mixing is what will prevent us from knowing in a real-world setting whether the difference is biological (treatment related) or simply noise (batch related).

    Now, if you’re thinking: why not include batch effect as a covariate in the linear model to remove its effect? Give it a try and see what happens! Depending on how you write the code, you should either get an “NA” (missing value) returned for your p-value for the treatment effect, or the same result as above (assuming the batch differences are large enough and enough samples).



    Scenario 2: Same as Scenario 1, although this time there is a large treatment effect alongside the large batch effect difference, and the samples are (again) not mixed between batches. This time, we want to reject the null hypothesis that their is no difference between the means of the placebo and the control, and the simulations lead to a rejection rate (this time interpreted as power) of around 90%! Why does this work? In this case, the batch effect does not obscure the signal of a true difference, but actually artificially adds to it. The problem in a real-world setting is that you don’t always know whether you’re in Scenario 1 or Scenario 2 just be examining the data. This is the real pitfall of not properly mixing your two groups between batches that can kill an experiment before any analysis is performed.

    Scenario 3: What if we have no treatment effect, but this time we put a mixture of treated and control patients in each of our two batches? In this scenario, we can visualize the difference between batch effects and the non-existent treatment effect. In the figure below, the first plot (top left) shows two distinct clusters of the molecular feature, but this time the two clusters are not perfectly separated by assignment to treatment and control groups! Instead, if we only consider the batch effects in the second plot (top right), we see that the two well-separated clusters in the data line up perfectly with which batch the data came from. These simple visuals are again helpful, because they suggest the main driver of the two clusters of data are due to batch effects and not a true biological (treatment) effect. In fact, failing to account for the batch assignment in our linear regression models leads to a rejection rate (this time FPR) of close to 1, far above our intended rate of .05. Conversely, if we include the batch assignment in our linear models alongside the treatment assignment, the FPR drops to .056.

  • Relearning OOP the fun way: slowly building a space-based game! (Part 1)

    A few years ago I wrote a maze-crawler game in C++ for a school project, but it was arguably the most stimulating work I’ve done to date. Statistics, data exploration/visualization, and math have their appeal for me, but there was something about coding a game into existence that brought real joy every time I brought the game closer to working. Don’t get me wrong: there were plenty of parts of my code that went wrong when I tried to turn my outline/pseudo-code into an actual game, but the first time my character moved (and the enemies on the same floor moved towards them) was exhilarating! There was a part of me that wanted to keep going down this route for a future career, but I’d already invested a lot of time/effort into training myself as a statistician, and eventually enough time passed without me thinking about this kind of work. But now, in this part of my blog, I’m going to work my way through OOP with Python by making a game where people have ships, belong to factions, and face off against each other.

    The first goal was to make some ship classes and do some testing of how they interact. As a step one, I made a ship class with a set of core attributes: a ship’s attack strength, armor value, and hitpoints. Then, a couple of core methods: an ability to attack (and record “dice” roles), and an ability to update hitpoints based on enemy attacks (“dice” roles). The ship parent class looks like this:

    # Ships will have a number of hitpoints, a number of dice to attack with, and an armor value that the...
# ... attacking ship must cross in order to land a hit.

class Ship:

    def __init__(self, armor, num_attacks, hitpoints):
        self.armor = armor
        self.num_attacks = num_attacks
        self.hitpoints = hitpoints

    # How many attacks pierced the armor?
    def take_damage(self, dice_values):
        # For each dice roll:
        for attack in range(len(dice_values)):
            if dice_values[attack] > self.armor:
                self.hitpoints -= 1
    # Generate random dice rolls. Number of dice rolls will be dependent on what subclass of...
    # ... ship is being used (and later what faction/bonuses are involved).
    def roll_dice(self):
        dice_values = []
        for dice in range(self.num_attacks):
            temp_dice_roll = random.randint(1,6)
            dice_values.append(temp_dice_roll)
        return dice_values

    From this parent class, I made two types (sub-classes) of ships: destroyers and cruisers. The destroyer has weaker attribute values than the cruiser, but the cruiser will have a higher cost, where the latter feature will start to matter as I fill out the details of the game/game board:

    # Each subtype of ship will have a cost attached to it. 

class Destroyer(Ship):

    # Here we add the cost of our sub-class
    cost = 2

    def __init__(self):
        # Use super to call ship's init, but then specify the destroyer's instance of...
        # ... armor, attacks, and hit points.
        super().__init__(armor=2, num_attacks=1, hitpoints=1)
    

class Cruiser(Ship):
    # Here we add the cost of our sub-class
    cost = 5



    def __init__(self):
        # Use super to call ship's init, but then specify the destroyer's instance of...
        # ... armor, attacks, and hit points.
        super().__init__(armor=3, num_attacks=1, hitpoints=2)

    Then I would simulate a simple “battle” of these two ship types against each other and record the fractions of times that, say, the destroyer won in a head-to-head fight with the cruiser. These tests help to sanity check that my code is working. For example, the destroyer is weaker than the cruiser, so I’d expect (on average) that the fraction of times that the destroyer wins should be less than 0.5 (and its fun to simulate things, so why not??):

    # Test 1: does 1 destroyer beat 1 cruiser? Simulate many times and record fraction...
# ... if times where the destroyer wins. Use this (and number of sims) to run a simple t-test...
# ... I will also let the destroyer go first (later tests can vary this!).

# More simulations to make the test results more conclusive.
sims = 1000

num_destroyer_wins = 0

for sim in range(sims):
    first_destroyer = Destroyer()
    #second_destroyer = Destroyer()

    first_cruiser = Cruiser()

    # Each round continues until one side is sunk
    while((first_destroyer.hitpoints > 0) and
          first_cruiser.hitpoints > 0 ):
        # Destroyer attacks:
        destroyer_roll1 = first_destroyer.roll_dice()
        #destroyer_roll2 = second_destroyer.roll_dice()
        # Just use "+" and no "[]" to concatenate!
        # all_destroyer_dice = destroyer_roll1 + destroyer_roll2
        all_destroyer_dice = destroyer_roll1

        # Check for a hit to cruiser:
        first_cruiser.take_damage(all_destroyer_dice)

        # If the cruiser is still alive, the cruiser attacks.
        if(first_cruiser.hitpoints > 0):
            cruiser_roll1 = first_cruiser.roll_dice()
            all_cruiser_dice = cruiser_roll1
            # check for hits to destroyer:
            first_destroyer.take_damage(all_cruiser_dice)
    
    # Who won?
    if first_destroyer.hitpoints > 0:
        num_destroyer_wins += 1

# What fraction of sims did the destroyer win?
fraction_destroyer_won = num_destroyer_wins/sims


# Perform binomial test
result = binomtest(num_destroyer_wins, sims, p=0.5, alternative='two-sided')

# Print results
print(f"Destroyer wins: {num_destroyer_wins} out of {sims}")
print(f"p-value: {result.pvalue:.4f}")

    The results show that the destroyer wins about 10% of all battles, but my cost ratio between these two ships is 2.5. If I change nothing else, this would suggest to me that cruisers are a better deal than destroyers, so future work will require some tinker of this. A couple future concerns are about how to assign hits when there are multiple ships in each group and/or ships can do more than one hit (e.g. does the defender/attack choose this, or can I set some rules about ships that automatically assign this?).

  • Simulations are your friend! Part I: the right kind of samples

    I work mostly with Biologists and MDs who seem to love their work. A typical project I’ve consulted for involves the collection of something called single-cell RNAseq data, which basically means collecting information about gene expression for each of the many cells (often greater than 10,000 cells) in a given sample. This technology still isn’t cheap, so getting samples from multiple people is far from trivial. If the goal was to compare the mean gene expression of a particular gene between a healthy control group and some diseased population, would 10,000 cells from one healthy patient and one patient with a disease be sufficient to make this comparison?

    The first time I encountered this question, I thought the answer was straightforward (one sample per group does not a meaningful statistical analysis make), but I wasn’t sure how to convince my non-statistician colleagues that this was the case. The hypothesis question was targeted at the patient level of our data, so you needed more patients, not just more cells. That’s when I decided to run a simple simulation and “prove” to them that my intuition was right!

    To show the issue, imagine I have two patients, one from a healthy control group and one from a disease group, and I’m only interested in one particular gene. In this scenario, let’s say that the true mean expression of this gene is the same in both groups. To simulate this, I draw two means from the same Poisson($\lambda$) distribution. Call these two observed draws HC for healthy control patient one’s mean and D for disease patient two’s mean. Then for each person I “sequence” a bunch of cells, where each cell’s gene expression is simulated by draws from either a Poisson(HC) distribution for patient one or a Poisson(D) distribution for patient two. Lastly, I take the mean observed expression values among the cells in each patient and do an unpaired t-test, where the sample sizes used are the total number of cells simulated above. Our goal was to test whether the disease and healthy control groups have different mean gene expressions, and since these two populations share the same mean we would hope that our test fails to reject the null hypothesis that the means are equal. However, if you repeat the simulation above many times with a reasonable number of cells (see code, but I think even 1000 cells is on the low end of most studies), the fraction of rejections of the null hypothesis is somewhere around 80% of all tests! Since the null hypothesis is true in every simulation run, this represents the false positive rate (FPR), and 80% is well above the intended FPR rate of 5%.

    This seemed like a good start towards proving my intuition, but I also wanted to show how adding more samples would bring the FPR back to its intended level. The first thing I did was to take 20 samples from each population and repeat the same process as above, using all the cells from these far more representative samples of each group to rerun the tests… but the FPR went up to 90%! Shame and despair crept in, and I fantasized about pursuing a professional badminton career about a decade too late in life. Then I realized I forgot my own intuition: what you needed was more measures at the sample level, not at the cell level. I needed to get sample means from each patient within each group, then average over these to run my t-test. The true sample size was the number of patients, not the number of cells. The latter were merely used to form the observations I needed to run the right test for the question I truly wanted to answer. And now… an FPR of .05 (well, sometimes in the range of .04-.06 depending on how many simulations I ran, but close enough to partially remove my shame from before)!

  • Statistics with me

    Documenting my time outside academia, mostly talking about statistics (or at least my attempt at discussing them in a meaningful manner).